解几何综合题这类问题时,要根据已知条件和给定图形的性质,通过计算和演绎推理,进行探究解决问题。这类问题是对初中数学知识的综合考察,涉及的知识有函数、有关三角形和四边形的性质,相似三角形、解三角形、圆等,涉及的问题如根据图形的运动和变化求函数关系式,并用所求的函数关系式进行进一步探究何时满足某些特殊条件(比如等腰三角形,直角三角形,平行四边形,等腰梯形等),或者是当某对三角形相似时满足什么条件,以及线段长度和图形面积之间的有关计算等等。
例题1
如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB=4/5,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
(1)当圆C经过点A时,求CP的长;
(2)联结AP,当AP//CG时,求弦EF的长;
(3)当△AGE是等腰三角形时,求圆C的半径长.
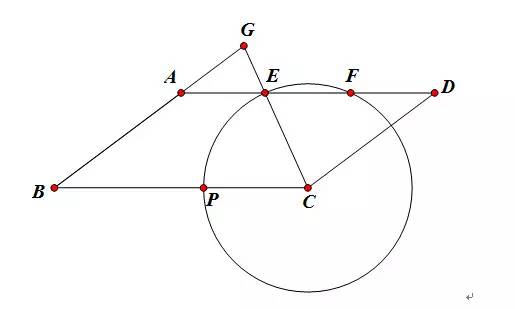
分析:第(1)题即求CA的长,根据条件AB=5,BC=8,cosB=4/5,解△ABC即可。

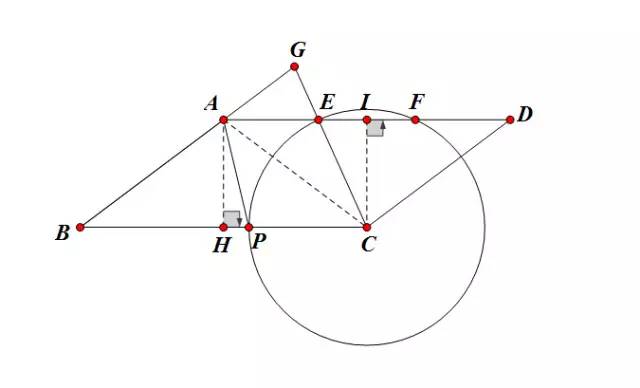
第(2)题由AP∥CG及圆的半径相等(CP=CE),可得四边形APCE是菱形,另外要求弦EF的长,可作弦心距CI。

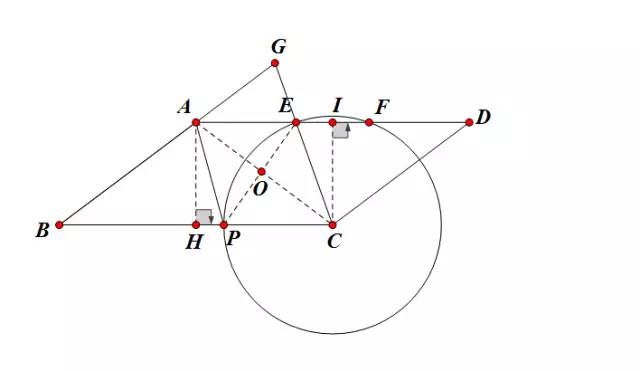
第(2)题也可以用如下方法:
注意到菱形的性质,可以联结菱形APCE的对角线,利用菱形的对角线互相垂直平分的性质。

当图形在运动过程中符合某种特殊条件,一定可以由这个条件推理出一些结论,再利用所得到的结论进行演绎推理或运算。
第(3)题有两种思路,注意到由△AGE是等腰三角形可以得到△CDE是等腰三角形。第1种方法可以设圆C的半径长为r,然后利用r计算出△CDE的各边边长,再根据△CDE是等腰三角形进行分类讨论。

第2种方法是利用△CDE是等腰三角形以及cosB=4/5两个条件,分三种情况解△CDE。


第(3)题的两种解法中,也可以直接求△AGE的三条边并进行分类讨论,但求解过程和结果比较复杂,由△AGE是等腰三角形得到△CDE是等腰三角形是解题的关键,可以大大简化计算,这种转化的方法在解综合题时很常用,应该好好体会。