求取值范围问题
近几年的中考题,我们经常遇到求参数取值范围的问题。解答这类题型时,如果能够将不等式问题转化为方程,往往会有出奇制胜的效果,不信你看看:
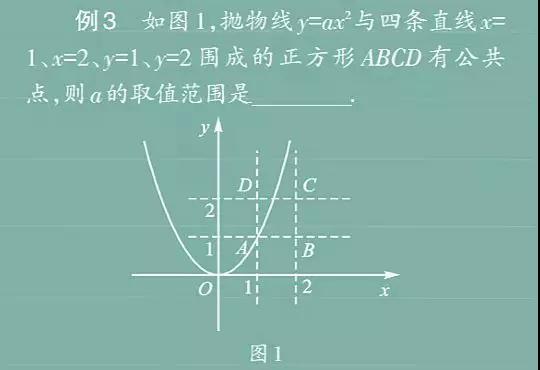
解析:本题答案是关于a的不等式。考虑到不等式的边界是方程,因此只需要考查两个极端情形:抛物线的开口变大时,有公共点和没有公共点的边界是点B(2,1);当抛物线的开口变小时,有公共点和没有公共点的边界是点D(1,2)。分别代入抛物线的解析式可得a1=1/4,a2=2,考虑到题目只关注有公共点,因此本题的答案是1/4a2。
再看例题4:

例题4如果运用常规解法是比较麻烦的:需要先解方程组,用a的代数式表示交点,然后再根据点在第二象限列出不等式组,最后解不等式组。如果同学们巧用方程和不等式的关系就可以简化解题过程。
例5如图2,已知射线DE与x轴和y轴分别交于点D(3,0)和点E(0,4),动点C从点M(5,0)出发,以1个单位长度每秒的速度沿x轴向左做匀速运动,以点C为圆心、[12t]个单位长度为半径作⊙C,设运动时间为t秒.当⊙C与射线DE有公共点时,求t的取值范围.

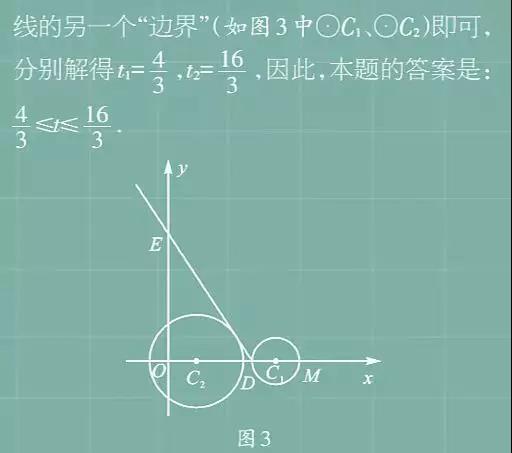
【分析】在⊙C的运动过程中,与射线DE的公共点个数分别是0个、1个、2个、1个、0个,因此,若要求t的取值范围,只要解决圆刚刚接触到射线的边界位置和圆即将脱离射线的另一个边界(如图3中⊙C1、⊙C2)即可,分别解得t1=[43],t2=[163],因此,本题的答案是:[43]t[163].
三、分类讨论问题
分类讨论题综合性强,在历年中考试题中多以压轴题出现,难度很大,对同学们的能力要求很高。在分类讨论的时候,最关键的是如何分类,确保不遗漏、不重复。我们利用方程和不等式的关系,利用数轴可以很好地解决这一难点。看例题6:

方程与不等式是相等与不等的代数情况,我们不但要理解性质,掌握解题的一般方法,还要熟能生巧。要领悟和掌握一些特殊的解题技巧和规律,在学习中必能事半功倍。